说起来,这篇文章中的大部分内容是我大二的时候琢磨的。本以为当年已经在某游戏论坛发了,打算找到之后重新写一下的时候发现,好像真的没有发。。。
当时打算写个系列,信誓旦旦的要写到第四篇,结果只发了两篇。。。(跟War3严重相关 ,如果你有兴趣的话,这里是 第一篇 和 第二篇)。
剩下的两篇一篇是TXT,今年夏天那个硬盘应该是坏了吧(pia ji 摔到了地上)。。。另外一篇当年还是手稿状态,所以。。。早都变成纸浆了把。
为了防止再次出现这个问题。。。我还是写篇文章,好歹记录下来吧。
郑重声明:本文及本系列文章(如果有的话)纯属本人脑补产物,如果在阅读过程中有任何不适,请立即点击右上角的红色按钮。本文可能的副作用包括口干舌燥、恶心、呕吐、积水、阵痛、幻觉、痴呆、精神病、昏迷、死亡和口臭。(借用了WAR3牧师的台词不好意思)
0x00 符号声明
战斗单位 某个单位或者由很多单位组成的部队或者是不管什么游戏角色,只要他能战斗就都叫做战斗单位
A 某个战斗单位通过一系列的基于游戏机制的运算,得到这个战斗单位的基本DPS (Damage Per Second)。对于由若干单位组成的部队,其值是各个单位DPS之和。
注意:需要计算的是实际伤害而非打出的攻击数值,在带有减伤或者加成机制游戏需要计算这个攻击力打到目标身上实际掉的生命值。
注意:大多数游戏中,这个将会是个恒定值,但是如果有战斗单位的攻击力会随着时间或者其它因素变化,这将是一个函数而非常量。但战损并不算在其中(因为本文就是讨论战损的影响的啊混蛋)。
注意:对于有随机成分的战斗机制,建议取其期望;对于和用户操作有关的战斗机制,建议统计其均数。
H 某个战斗单位的总生命值(能够承受伤害的总值)。对于由若干单位组成的部队,其值是各个单位生命值之和。
f(t) f(t) 在本文中表示某个战斗单位的实际DPS随战斗时间变化的函数。
h(t) h(t) 在本文中表示某个战斗单位的实际生命值随战斗时间变化的函数。
显然的,有下式成立:
$$
h(t) = H - \Delta H = H - \int_ {0}^{t} f(x)dx
$$
(式1) 注意:此处f(x)为敌方的f(t)
0x01 一个简单的情况
在大多数游戏的战斗中,某一个战斗单位的实际DPS是与其当前生命值无关的,在战斗过程中都是恒定。譬如在回合制或半回合制RPG游戏中,角色的伤害并不因为受伤了而变少或变多;又或者RTS游戏中两个兵单挑;又或者魔法门英雄无敌中两个大天使对砍;又或者两队大和一一捉对对打(你俩操作是有多差啊喂!)。
这种情况下f(t)显然是个恒定值
$$
f_1(t) = A_1
$$
$$
f_2(t) = A_2
$$
带入式1得到:
$$
h_1(t) = H_1 - A_2t
$$
$$
h_2(t) = H_2 - A_1t
$$
两个常数函数和两个一次函数而已
如下是 H_1 = H_2 = 100 , A_1 = 8, A_2 = 10 情况下的函数图像
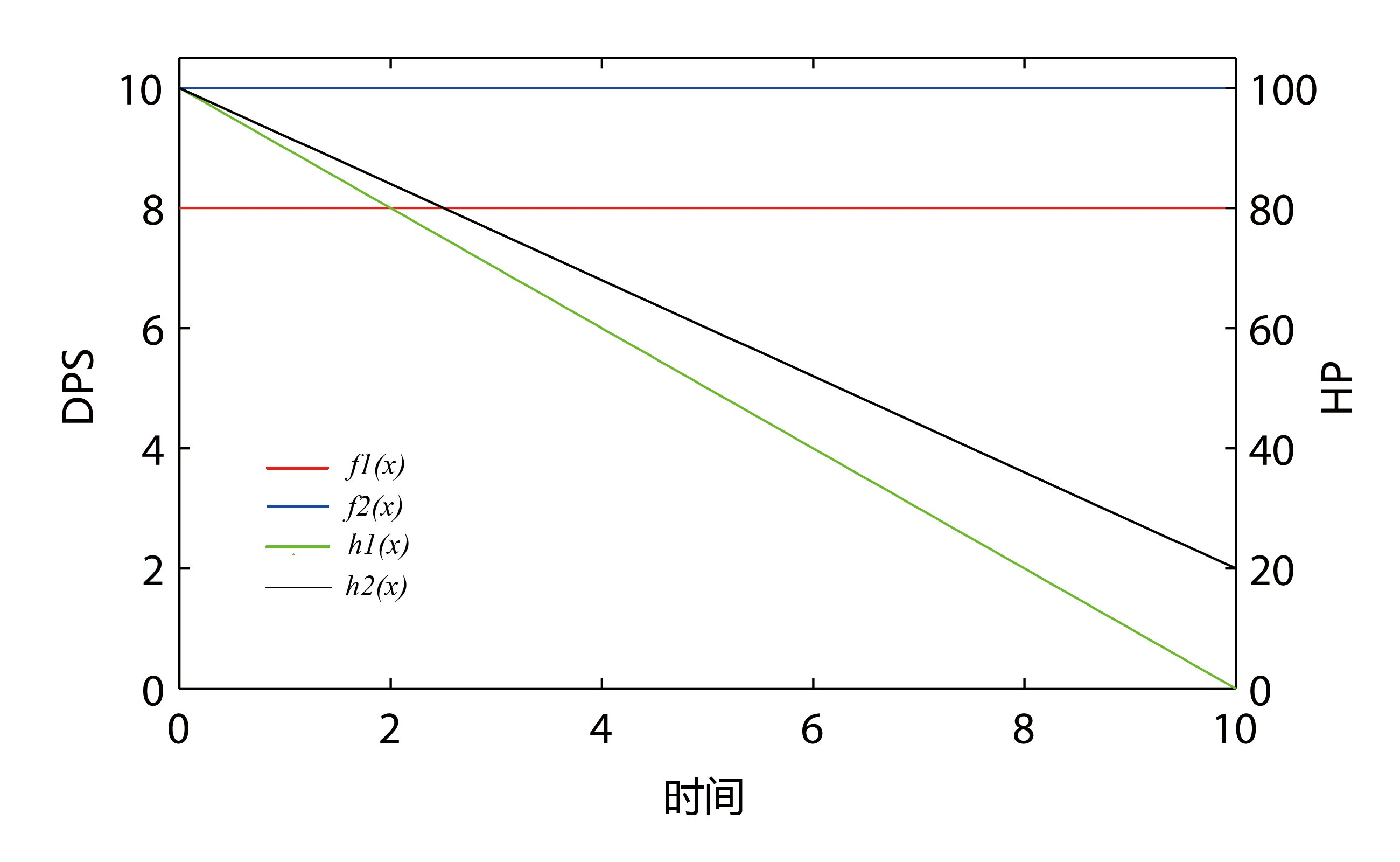
0x02 一个有点复杂的情况
在RTS和其他策略类游戏中,战斗单位往往不是一个小兵,而是一支部队。这样部队的DPS往往就正比于小兵的数量。这样在将部队看做一个整体(战斗单位)的情况下,把这个情况理想化,假定每个小兵的生命值都是1。于是得到下式子成立:
$$
f(t) = \frac {h(t)} {H} A
$$
(式 2)
现在假定部队1只有一个单位,部队2为符合上述模型的部队。例如星际2中一群枪兵打开了大炮台的神族基地,或者是魔法门英雄无敌中大天使单挑一队弩手。f1就应该是恒定值A1;f2则应该用式2表示,然后带入式子1得到:
$$
f_1(t) = A_1
$$
$$
f_2(t) = \frac {h_2(t)} {H_2} A_2 = A_2 \frac{H_2 - \int_ {0}^{t} f_1(x)dx}{H_2} = A_2(1 - \frac{A_1t}{H_2})
$$
显然是f2个一次函数。根据式1知道,h1、h2分别仅与f2、f1的积分线性相关,所以显然h2是一个一次函数,而h1是一个二次函数
$$
h_1(t) = H_1 - A_2(t - \frac{A_1}{2H_2} t^2)
$$
$$
h_2(t) = H_2 - A_1t
$$
如下是 H_1 = H_2 = 100 , A_1 = A_2 = 10 情况下的函数图像
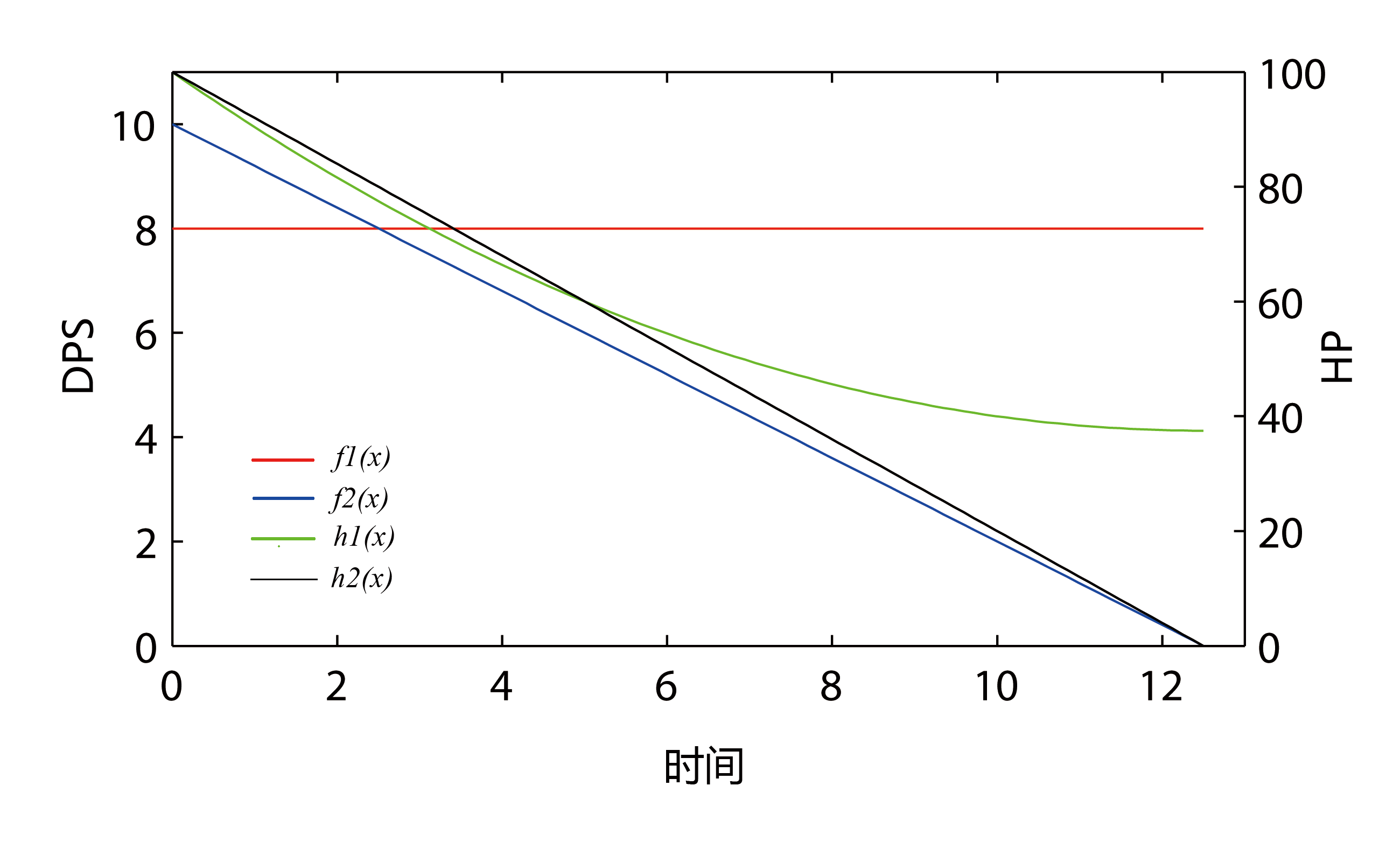
0x03 一个棘手的情况
然而,RTS和策略类游戏中更多的情况是两支部队对打,这样情况就会相当复杂。同上例部队f_2(t)函数的分析过程,可以得到两支部队的f函数
$$
f_1 (t)=A_1 \frac {H_1 - \int_{0}^{t} f_2(x) dx} {H_1}
$$
$$
f_2 (t)=A_2 \frac {H_2 - \int_{0}^{t} f_1(x) dx} {H_2}
$$
将f2带入f1得:
$$
f_1(t)=A_1- \frac {A_1}{H_1} \int_ {0}^{t}(A_2-\frac{A_2}{H_2} \int_ {0}^{x} f_1(y)dy)dx
$$
数学渣渣的我当年在这一步根本解不下去了,于是就这么从当年放置Play到现在。 感谢感谢果壳网的 @LePtC 同学在这里的帮助,完整的解答过程请看那个帖子。总之两次求导并解其微分方程得
$$
f_1(t)=A_1cosh(\sqrt{\frac{A_1A_2}{H_1H_2}}t)-A_2\sqrt{\frac{H_2A_1}{H_1A_2}}sinh(\sqrt{\frac{A_1A_2}{H_1H_2}}t)
$$
$$
f_2(t)=A_2cosh(\sqrt{\frac{A_1A_2}{H_1H_2}}t)-A_1\sqrt{\frac{H_1A_2}{H_2A_1}}sinh(\sqrt{\frac{A_1A_2}{H_1H_2}}t)
$$
令:
$$
\lambda = \sqrt{\frac{A_1A_2}{H_1H_2}}
$$
有
$$
f_1(t)=A_1cosh(\lambda t)-\lambda H_2sinh(\lambda t)
$$
$$
f_2(t)=A_2cosh(\lambda t)-\lambda H_1 sinh(\lambda t)
$$
并带入(式1)得
$$
h_1(t)= H_1cosh(\lambda t) - \frac{A_2}{\lambda} sinh(\lambda t)
$$
$$
h_2(t)= H_2cosh(\lambda t) - \frac{A_1}{\lambda} sinh(\lambda t)
$$
同样的,在 H_1 = H_2 = 100 , A_1 = 8, A_2 = 10 情况下的函数图像
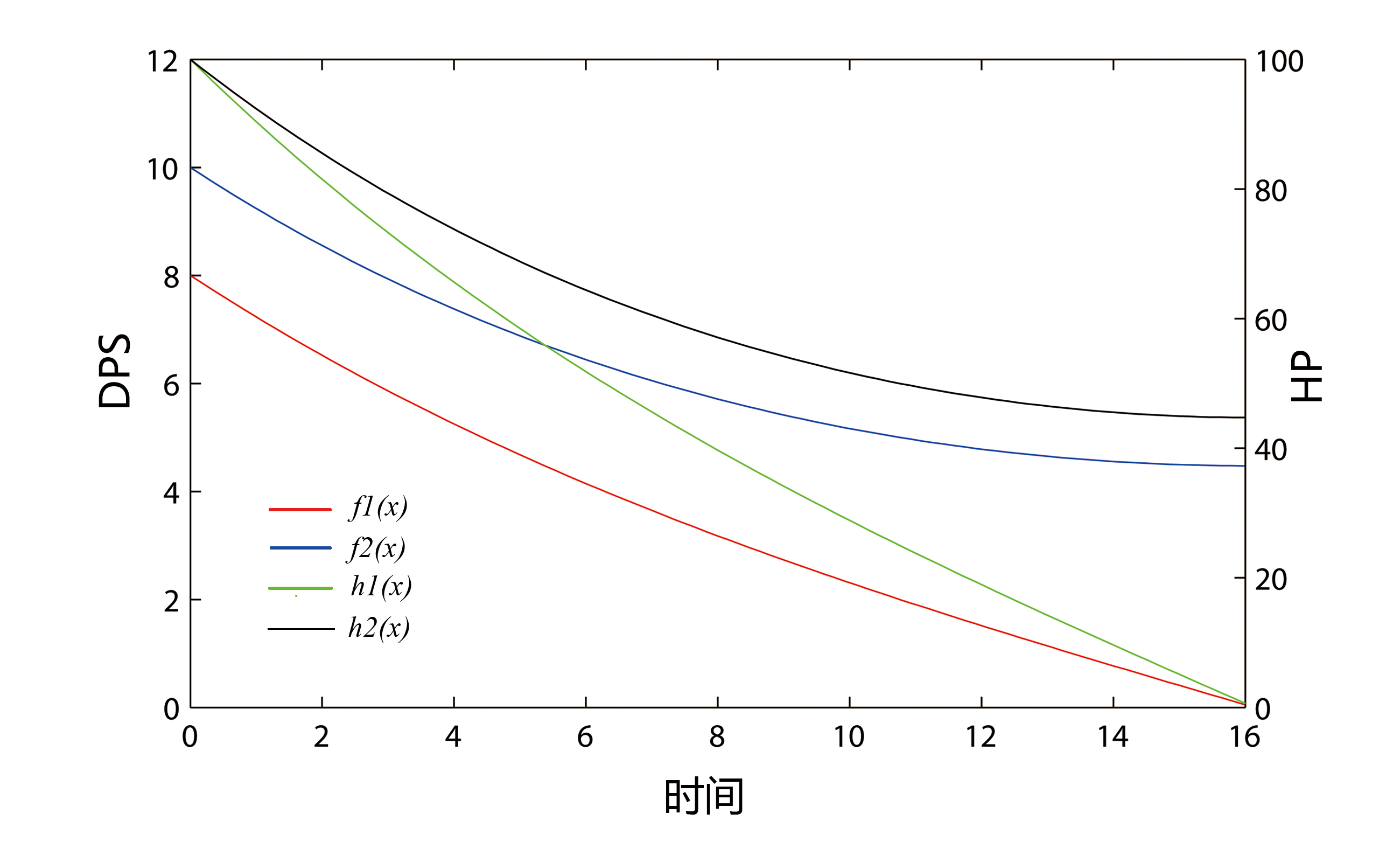
There are comments.